~前回のあらすじ~
駒の動きを関数でまとめてみた。
今回は他の駒を増やすといいましたが、
その前に、まだバグが発生しているので直すことを考えましょう。。。
以下の例を見てください。
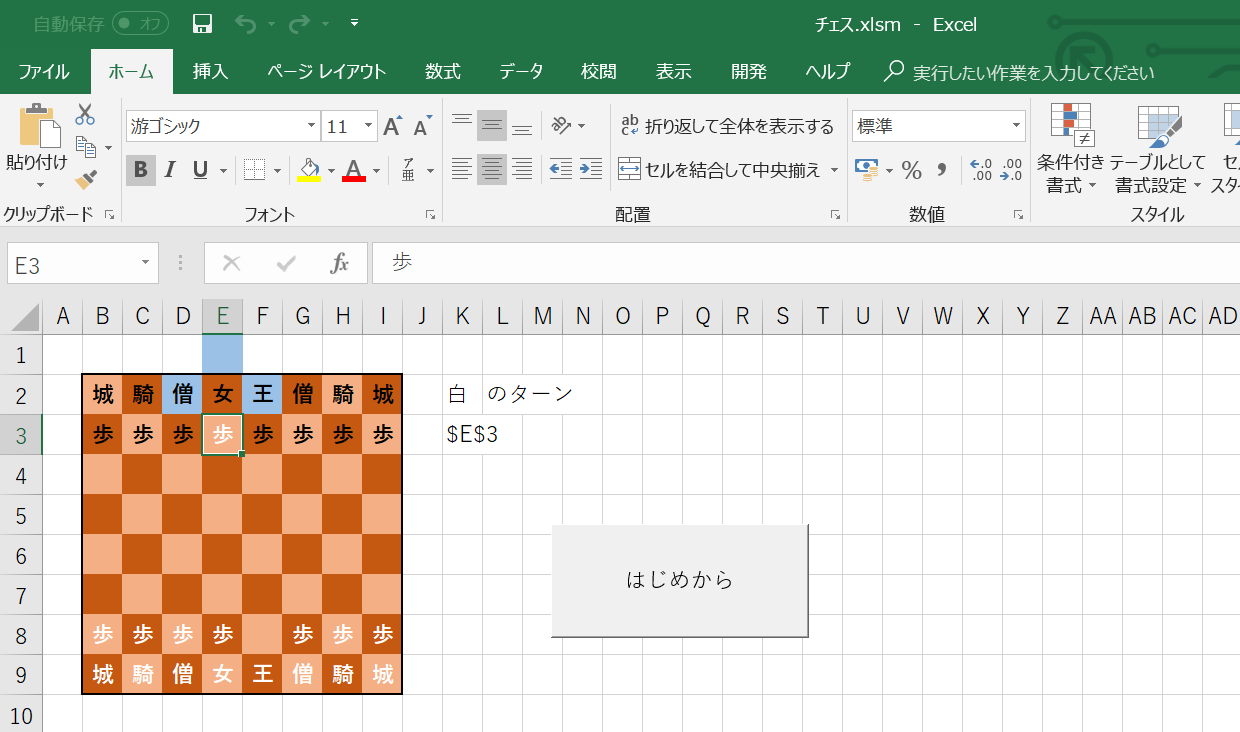
ポーンをひたすら上に動かし続けると。。。
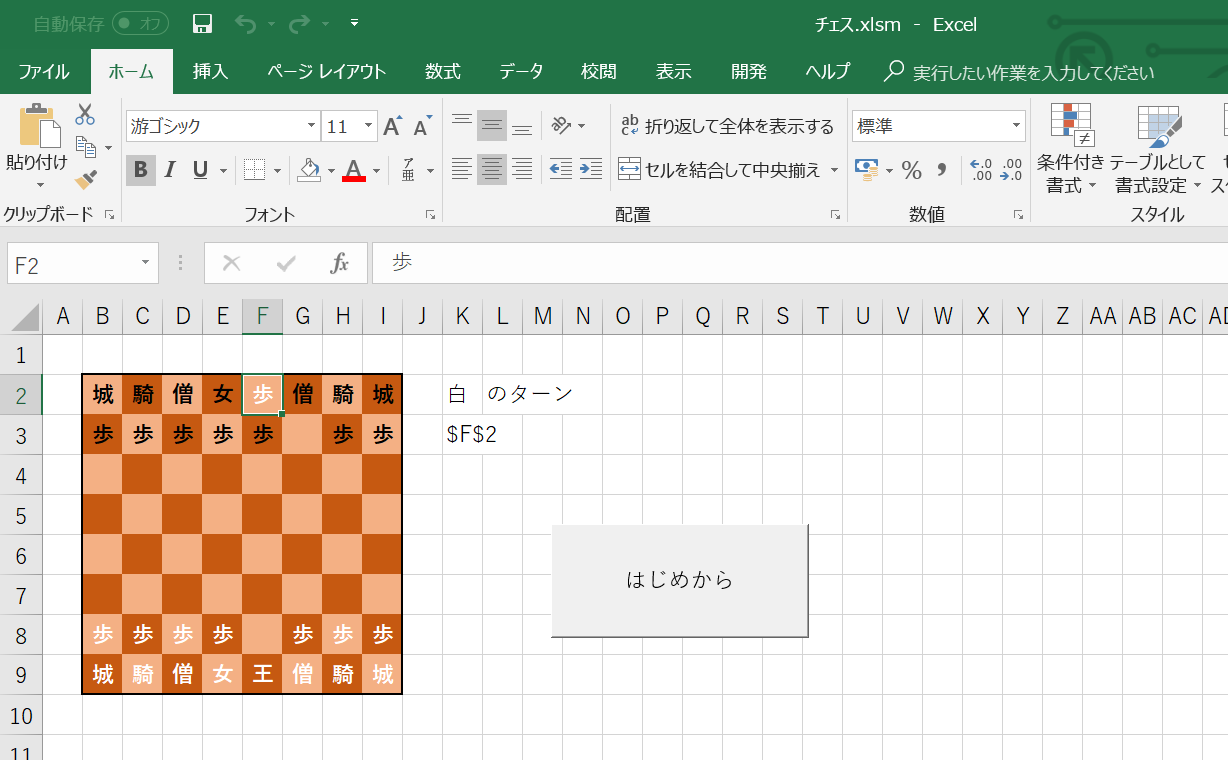
水色が上にはみ出しました。
この時点でかなりおかしいですがそれを無視してさらに上に動かすと。。。
エラーがでました。
上にセルがないからですね。
これを修正するには、水色になる範囲を決めてあげる必要があります。
関数を呼び出す側で、水色の範囲をApplication.Intersectで指定し、
戻り値で水色になるセルの行、列の配列を取得します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Dim Board As Range 'チェス盤の起点セル(左上)' Set Board = Range("B2") Dim blueCells() As Long If target.Value = "歩" And target.Font.Color = Piece_Color_W Then blueCells() = 白のポーン(target, Piece_Color_W, Piece_Color_B) Piece.Value = target.Address End If If Not UBound(blueCells, 1) = 0 Then '水色にするセルがあれば処理' For i = 0 To UBound(blueCells, 2) If Not Application.Intersect(Cells(blueCells(0, i), blueCells(1, i)), Range(Board, Board.Offset(7, 7))) Is Nothing Then Cells(blueCells(0, i), blueCells(1, i)).Interior.Color = SelectInterior_Color End If Next End If |
関数もがっつり変えちゃいましょう。
行、列の配列の値を返せるよう、FunctionうんぬんAs Long()にします。
上のblueCells()に返してあげます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
Function 白のポーン(ByVal target As Range, Piece_Color_W As Long, Piece_Color_B As Long) As Long() Dim i As Long Dim result() As Long Dim arr As Variant i = 0 m = target.Column arr = Array(-1, -2) For j = 0 To 1 n = target.row + arr(j) If n > 0 And m > 0 Then 'セルの存在チェック' If Cells(n, m).Value = "" Then If j = 1 And Cells(n + 1, m).Value "" Then Else ReDim Preserve result(1, i) result(0, i) = n result(1, i) = m i = i + 1 End If End If End If Next n = target.row - 1 arr = Array(-1, 1) For j = 0 To 1 m = target.Column + arr(j) If n > 0 And m > 0 Then 'セルの存在チェック' If Cells(n, m).Value "" And Cells(n, m).Font.Color = Piece_Color_B Then ReDim Preserve result(1, i) result(0, i) = n result(1, i) = m i = i + 1 End If End If Next If i = 0 Then ReDim Preserve result(0, 0) '水色にするセルがなかったらゼロの添字で判定' Else End If 白のポーン = result() End Function |
最後に白のポーン = 値にしてあげると、行、列の配列が取得できます。
これが戻り値ですね。呼び出し元にこの値を渡します。
これで実行すると。。。
できました。エラーが起きません。
さて、この調子で他の駒も作っていきますよ。
次回(こそ)は、作成したすべての駒の関数をご紹介します。
作ったものはGitHubにおいてありますのでみてね。
ではまた次回!